本文参考：https://www.pytorchmaster.com/

torch函数

torch.cat()

函数目的： 在给定维度上对输入的张量序列seq 进行连接操作。

outputs = torch.cat(inputs, dim=?) → Tensor

参数

  • inputs : 待连接的张量序列，可以是任意相同Tensor类型的python 序列
  • dim : 选择的扩维, 必须在0到len(inputs[0])之间，沿着此维连接张量序列。

重点

  1. 输入数据必须是序列，序列中数据是任意相同的shape的同类型tensor
  2. 维度不可以超过输入数据的任一个张量的维度

例子

  1. 准备数据，每个的shape都是[2,3]
1
2
3
4
5
6
x1 = torch.tensor([[11,21,31],[21,31,41]],dtype=torch.int)
x1.shape # torch.Size([2, 3])


x2 = torch.tensor([[12,22,32],[22,32,42]],dtype=torch.int)
x2.shape  # torch.Size([2, 3])
  1. 合成inputs
1
2
3
4
5
6
7
8
' inputs为２个形状为[2 , 3]的矩阵 '
inputs = [x1, x2]
print(inputs)
'打印查看'
[tensor([[11, 21, 31],
         [21, 31, 41]], dtype=torch.int32),
 tensor([[12, 22, 32],
         [22, 32, 42]], dtype=torch.int32)]
  1. 查看结果, 测试不同的dim拼接结果
1
2
3
4
5
6
7
8
In    [1]: torch.cat(inputs, dim=0).shape
Out   [1]: torch.Size([4,  3])

In    [2]: torch.cat(inputs, dim=1).shape
Out   [2]: torch.Size([2, 6])

In    [3]: torch.cat(inputs, dim=2).shape
IndexError: Dimension out of range (expected to be in range of [-2, 1], but got 2)

torch.stack()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
import torch

T1 = torch.tensor([[1, 2, 3],
                [4, 5, 6],
                [7, 8, 9]])
T2 = torch.tensor([[10, 20, 30],
                [40, 50, 60],
                [70, 80, 90]])

T3 = torch.stack((T1,T2),dim=0)
print(T3.shape)
print(T3)

'''
torch.Size([2, 3, 3])
tensor([[[ 1,  2,  3],
         [ 4,  5,  6],
         [ 7,  8,  9]],

        [[10, 20, 30],
         [40, 50, 60],
         [70, 80, 90]]])
'''

T4 = torch.stack((T1,T2),dim=1)
print(T4.shape)
print(T4)
'''
torch.Size([3, 2, 3])
tensor([[[ 1,  2,  3],
         [10, 20, 30]],

        [[ 4,  5,  6],
         [40, 50, 60]],

        [[ 7,  8,  9],
         [70, 80, 90]]])
'''

T5 = torch.stack((T1,T2),dim=2)
print(T5.shape)
print(T5)
'''
torch.Size([3, 3, 2])
tensor([[[ 1, 10],
         [ 2, 20],
         [ 3, 30]],

        [[ 4, 40],
         [ 5, 50],
         [ 6, 60]],

        [[ 7, 70],
         [ 8, 80],
         [ 9, 90]]])
'''

torch.ones_like()

torch.zeros_like()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
input = torch.rand(2, 3)
print(input)
# 生成与input形状相同、元素全为1的张量
a = torch.ones_like(input)
print(a)
# 生成与input形状相同、元素全为0的张量
b = torch.zeros_like(input)
print(b)

'''
tensor([[0.1362, 0.6439, 0.3817],
        [0.0971, 0.3498, 0.8780]])
tensor([[1., 1., 1.],
        [1., 1., 1.]])
tensor([[0., 0., 0.],
        [0., 0., 0.]])
'''

torch.range()

torch.arange()

1
2
3
4
5
6
7
8
9
10
11
>>> y=torch.range(1,6)
>>> y
tensor([1., 2., 3., 4., 5., 6.])
>>> y.dtype
torch.float32

>>> z=torch.arange(1,6)
>>> z
tensor([1, 2, 3, 4, 5])
>>> z.dtype
torch.int64

注意：

torch.range必须有begin和end值

但是torch.arange可以只有单值或设置间隔值

1
2
3
4
5
>> torch.arange(4)
>> tensor([0, 1, 2, 3])

>> torch.arange(1,0.6,-0.1)
>> tensor([1.0000, 0.9000, 0.8000, 0.7000])

torch.normal()

原型：normal(mean, std, *, generator=None, out=None)

该函数返回从单独的正态分布中提取的随机数的张量，该正态分布的均值是mean，标准差是std。

1
2
3
4
5
torch.normal(mean=torch.arange(4.),std=torch.arange(1.,0.6,-0.1)).reshape(2,2)
'''
tensor([[-1.4455,  0.9446],
        [ 3.2138,  3.3914]])
'''

张量

数据类型

基本上趋同于numpy.array，但是不支持str!!! 包括：

1
2
3
4
5
6
7
8
9
torch.float64(torch.double),
torch.float32(torch.float),
torch.float16,
torch.int64(torch.long),
torch.int32(torch.int),
torch.int16,
torch.int8,
torch.uint8,
torch.bool

一般神经网络都是用torch.float32类型

几种构造方式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import torch
import numpy as np

# 自动推断
a = torch.tensor(2.0)
print(a,a.dtype)
# tensor(2.) torch.float32

# 指定数据类型
b = torch.tensor(2.0, dtype=torch.double)
print(b,b.dtype)
# tensor(2.,dtype=torch.float64) torch.float64

#使用特定构造函数 & numpt转tensor
c = torch.IntTensor(1)
d = torch.Tensor(np.array(2.0))  #等价于torch.FloatTensor
e = torch.BoolTensor(np.array([1,0,2,0]))
print(c,c.dtype)
print(d,d.dtype)
print(e,e.dtype)
'''
tensor([5], dtype=torch.int32) torch.int32
tensor(2.) torch.float32
tensor([ True, False,  True, False]) torch.bool
'''

# 不同类型转换
i = torch.tensor(1); print(i,i.dtype)
x = i.float(); print(x,x.dtype) #调用 float方法转换成浮点类型
y = i.type(torch.float); print(y,y.dtype) #使用type函数转换成浮点类型
z = i.type_as(x);print(z,z.dtype) #使用type_as方法转换成某个Tensor相同类型

'''
tensor(1) torch.int64
tensor(1.) torch.float32
tensor(1.) torch.float32
tensor(1.) torch.float32
'''

张量的维度

不同类型数据会是不同的维度，有几层中括号就是多少维张量

标量为0维张量，向量为1维张量，矩阵为2维张量，彩色图像有rgb三个通道为3维张量，视频还有时间维表示为4维张量。

1
2
3
4
5
6
scalar = torch.tensor(True) # 0维
vector = torch.tensor([1.0,2.0,3.0,4.0]) #向量，1维张量
matrix = torch.tensor([[1.0,2.0],[3.0,4.0]]) #矩阵, 2维张量
tensor3 = torch.tensor([[[1.0,2.0],[3.0,4.0]],[[5.0,6.0],[7.0,8.0]]])  # 3维张量
tensor4 = torch.tensor([[[[1.0,1.0],[2.0,2.0]],[[3.0,3.0],[4.0,4.0]]],
                        [[[5.0,5.0],[6.0,6.0]],[[7.0,7.0],[8.0,8.0]]]])  # 4维张量

张量的尺寸

  • 使用shape属性或者size()方法查看张量在每一维的长度
  • 使用view()方法改变张量的尺寸,view()和numpy中的reshape很像，所以view()失败可以直接使用reshape
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 有些操作会让张量存储结构扭曲，直接使用view会失败，可以用reshape方法
matrix26 = torch.arange(0,12).view(2,6)
print(matrix26)       # tensor([[ 0,  1,  2,  3,  4,  5],
        			  #			[ 6,  7,  8,  9, 10, 11]])
print(matrix26.shape) # torch.Size([2, 6])

# 转置操作让张量存储结构扭曲
matrix62 = matrix26.t()
print(matrix62.is_contiguous()) # False

# 直接使用view方法会失败，可以使用reshape方法
#matrix34 = matrix62.view(3,4) #error!
matrix34 = matrix62.reshape(3,4) #等价于matrix34 = matrix62.contiguous().view(3,4)
print(matrix34) 
'''
tensor([[ 0,  6,  1,  7],
        [ 2,  8,  3,  9],
        [ 4, 10,  5, 11]])
'''

is_contiguous()：Tensor底层一维数组元素的存储顺序与Tensor按行优先一维展开的元素顺序是否一致

行有限列有限博客：https://zhuanlan.zhihu.com/p/64551412

张量和numpy数组

numpy –> tensor

  • 用numpy方法从Tensor得到numpy数组
  • 用torch.from_numpy从numpy数组得到Tensor

这两种方法关联的tensor和numpy数组是共享数据内存的，改变一个也会改变另一个。当然需要的话可以通过张量的clone方法拷贝张量中断这种关联。

此外可以使用item方法从标量张量得到对应的Python数值

​ 使用tolist方法从张量得到对应的Python数值列表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# ndarray->tensor
arr = np.zeros(3)
tensor = torch.from_numpy(arr)

# tensor->ndarray
tensor = torch.zeros(3)
arr = tensor.numpy()

# 可以用clone() 方法拷贝张量，中断这种关联
tensor = torch.zeros(3)
arr = tensor.clone().numpy() # 也可以使用tensor.data.numpy()

# item方法和tolist方法可以将张量转换成Python数值和数值列表
scalar = torch.tensor(1.0)
s = scalar.item()
print(type(s),' ',s)
# <class 'float'> 1.0

tensor = torch.rand(2,2)
t = tensor.tolist()
print(type(t),' ',t)
<class 'list'> [[0.8211846351623535, 0.20020723342895508], [0.011571824550628662, 0.2906131148338318]]

autograd自动微分

神经网络通常依靠反向传播求梯度更新网络参数，pytorch通过反向传播backward方法实现梯度计算，可以调用torch.autograd.grad函数来实现梯度计算，这就是Pytorch的自动微分机制

backward求导数

backward 方法通常在一个标量张量上调用，该方法求得的梯度将存在对应自变量张量的grad属性下。

如果调用的张量非标量，则要传入一个和它同形状 的gradient参数张量。

相当于用该gradient参数张量与调用张量作向量点乘，得到的标量结果再反向传播。

  1. 标量的反向传播
1
2
3
4
5
6
7
8
9
10
11
12
13
import numpy as np
import torch

# f(x) = a*x**2 + b*x + c的导数
x = torch.tensor(0.0,requires_grad = True) # x需要被求导
a = torch.tensor(1.0)
b = torch.tensor(-2.0)
c = torch.tensor(1.0)
y = a*torch.pow(x,2) + b*x + c 

y.backward()
dy_dx = x.grad
print(dy_dx) # tensor(-2.)
  1. 非标量的反向传播
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import numpy as np 
import torch 

# f(x) = a*x**2 + b*x + c
x = torch.tensor([[0.0,0.0],[1.0,2.0]],requires_grad = True) # x需要被求导
a = torch.tensor(1.0)
b = torch.tensor(-2.0)
c = torch.tensor(1.0)
y = a*torch.pow(x,2) + b*x + c 

gradient = torch.tensor([[1.0,1.0],[1.0,1.0]])

print("x:\n",x)
print("y:\n",y)
y.backward(gradient = gradient)
x_grad = x.grad
print("x_grad:\n",x_grad)

'''
x:
 tensor([[0., 0.],
        [1., 2.]], requires_grad=True)
y:
 tensor([[1., 1.],
        [0., 1.]], grad_fn=<AddBackward0>)
x_grad:
 tensor([[-2., -2.],
        [ 0.,  2.]])
'''
  1. 非标量的反向传播可以用标量的反向传播实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import numpy as np 
import torch 

# f(x) = a*x**2 + b*x + c

x = torch.tensor([[0.0,0.0],[1.0,2.0]],requires_grad = True) # x需要被求导
a = torch.tensor(1.0)
b = torch.tensor(-2.0)
c = torch.tensor(1.0)
y = a*torch.pow(x,2) + b*x + c 

gradient = torch.tensor([[1.0,1.0],[1.0,1.0]])
z = torch.sum(y*gradient)

print("x:",x)
print("y:",y)
z.backward()
x_grad = x.grad
print("x_grad:\n",x_grad)

'''
x: tensor([[0., 0.],
        [1., 2.]], requires_grad=True)
y: tensor([[1., 1.],
        [0., 1.]], grad_fn=<AddBackward0>)
x_grad:
 tensor([[-2., -2.],
        [ 0.,  2.]])
'''
  • 在numpy和torch.tensor中 * 都是指相同size的矩阵各个位置相乘产生新矩阵
  • numpy中的矩阵乘法为np.dot(a,b)，torch中为torch.matmul(c,d)

autograd.grad自动微分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import numpy as np 
import torch 

# f(x) = a*x**2 + b*x + c的导数
x = torch.tensor(0.0,requires_grad = True) # x需要被求导
a = torch.tensor(1.0)
b = torch.tensor(-2.0)
c = torch.tensor(1.0)
y = a*torch.pow(x,2) + b*x + c

# create_graph 设置为 True 将允许创建更高阶的导数 
dy_dx = torch.autograd.grad(y,x,create_graph=True)[0]
print(dy_dx.data)      # tensor(-2.)

# 求二阶导数
dy2_dx2 = torch.autograd.grad(dy_dx,x)[0] 
print(dy2_dx2.data) # tensor(2.)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import numpy as np 
import torch 

x1 = torch.tensor(1.0,requires_grad = True) # x需要被求导
x2 = torch.tensor(2.0,requires_grad = True)

y1 = x1*x2
y2 = x1+x2


# 允许同时对多个自变量求导数
(dy1_dx1,dy1_dx2) = torch.autograd.grad(outputs=y1,inputs = [x1,x2],retain_graph = True)
print(dy1_dx1,dy1_dx2)
# tensor(2.) tensor(1.)

# 如果有多个因变量，相当于把多个因变量的梯度结果求和
(dy12_dx1,dy12_dx2) = torch.autograd.grad(outputs=[y1,y2],inputs = [x1,x2])
print(dy12_dx1,dy12_dx2)
# tensor(3.) tensor(2.)

利用autograd和optimizer求最小值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import numpy as np
import torch

# f(x) = a*x**2 + b*x + c的最小值
x = torch.tensor(0.0, requires_grad = True) # x需要被求导
a = torch.tensor(1.0)
b = torch.tensor(-2.0)
c = torch.tensor(1.0)

optimizer = torch.optim.SGD(params=[x], lr=0.01)

def f(x):
    result = a*torch.pow(x,2) + b*x + c
    return (result)
for i in range(500):
    optimizer.zero_grad()
    y = f(x)
    y.backward()
    optimizer.step()
    
print(f"y= {f(x).data}; x= {x.data}") # f-string格式化
# y= tensor(0.) ; x= tensor(1.0000)

动态计算图

之前的一些深度学习框架使用静态计算图，而pytorch使用动态计算图，有它的优点

动态图简介

img

pytorch的计算图由节点和边组成，节点表示张量或Function,边表示张量和Function之间的依赖关系

动态有两重含义

  • 计算图正向传播是立即执行的，无需等待完整的计算图创建完毕，每条语句都会在计算图中动态添加节点和边，并立即执行正向传播得到的计算结果。
  • 计算图在反向传播后立即销毁。下次调用需要重新构建计算图。如果在程序中使用了backward方法执行了反向传播，或者利用torch.autograd.grad方法计算了梯度，那么创建的计算图会被立即销毁，释放存储空间，下次调用需要重新创建

1.计算图的正向传播是立即执行的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import torch 
w = torch.tensor([[3.0,1.0]],requires_grad=True)
b = torch.tensor([[3.0]],requires_grad=True)
X = torch.randn(10,2)
Y = torch.randn(10,1)
Y_hat = X@w.t() + b  # Y_hat定义后其正向传播被立即执行，与其后面的loss创建语句无关
loss = torch.mean(torch.pow(Y_hat-Y,2))

print(loss.data)
print(Y_hat.data)

'''
tensor(17.8969)
tensor([[3.2613],
        [4.7322],
        [4.5037],
        [7.5899],
        [7.0973],
        [1.3287],
        [6.1473],
        [1.3492],
        [1.3911],
        [1.2150]])
'''

2.计算图在反向传播后立即销毁

1
2
3
4
5
6
7
8
9
10
import torch 
w = torch.tensor([[3.0,1.0]],requires_grad=True)
b = torch.tensor([[3.0]],requires_grad=True)
X = torch.randn(10,2)
Y = torch.randn(10,1)
Y_hat = X@w.t() + b  # Y_hat定义后其正向传播被立即执行，与其后面的loss创建语句无关
loss = torch.mean(torch.pow(Y_hat-Y,2))

#计算图在反向传播后立即销毁，如果需要保留计算图, 需要设置retain_graph = True
loss.backward()  #loss.backward(retain_graph = True) 
1
loss.backward() #如果再次执行反向传播将报错

RuntimeError: Trying to backward through the graph a second time (or directly access saved tensors after they have already been freed). Saved intermediate values of the graph are freed when you call .backward() or autograd.grad(). Specify retain_graph=True if you need to backward through the graph a second time or if you need to access saved tensors after calling backward.

第二次尝试向后遍历图形（或在张量已被释放后直接访问已保存的张量）。当您调用 .backward() 或 autograd.grad() 时，图形的已保存中间值将被释放。如果您需要第二次向后遍历图形，或者如果您需要在向后调用后访问保存的张量，请指定 retain_graph=True。

计算图中的Function

计算图中除了张量的另外一种节点是Function, 实际上就是 Pytorch中各种对张量操作的函数

这些Function和我们python中的函数有一个较大的区别，那就是它同时包含正向计算逻辑和反向传播逻辑

我们可以通过继承torch.autograd.Function来创建这种支持反向传播的Function

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class MyReLU(torch.autograd.Function):
    # 正向传播逻辑，可以用ctx存储一些值，供反向传播使用
    @staticmethod
    def forward(ctx, input):
        ctx.save_for_backward(input)
        return input.clamp(min=0)
    
    # 反向传播逻辑
    @staticmethod
    def backward(ctx, grad_output):
        input, = ctx.saved_tensors
        grad_input = grad_output.clone()
        grad_input[input < 0] = 0
        return grad_input
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import torch 
w = torch.tensor([[3.0,1.0]],requires_grad=True)
b = torch.tensor([[3.0]],requires_grad=True)
X = torch.tensor([[-1.0,-1.0],[1.0,1.0]])
Y = torch.tensor([[2.0,3.0]])

relu = MyReLU.apply # relu现在也可以具有正向传播和反向传播功能
Y_hat = relu(X@w.t() + b)
loss = torch.mean(torch.pow(Y_hat-Y,2))

loss.backward()

print(w.grad)	#tensor([[4.5000, 4.5000]])
print(b.grad)	#tensor([[4.5000]])

# Y_hat的梯度函数即是我们自己所定义的 MyReLU.backward
print(Y_hat.grad_fn)	#<torch.autograd.function.MyReLUBackward object at 0x1205a46c8>

计算图与反向传播

简单理解反向传播的原理和过程（链式法则）

1
2
3
4
5
6
7
8
import torch

x = torch.tensor(3.0, requires_grad=True)
y1 = x + 1
y2 = 2*x
loss = (y1-y2)**2

loss.backward()

loss.backward()语句调用后，依次发生以下计算过程。

  1. loss自己的grad梯度赋值为1，即对自身的梯度为1。

  2. loss根据其自身梯度以及关联的backward方法，计算出其对应的自变量即y1和y2的梯度，将该值赋值到y1.grad和y2.grad。

  3. y2和y1根据其自身梯度以及关联的backward方法, 分别计算出其对应的自变量x的梯度，x.grad将其收到的多个梯度值累加。

（注意，1,2,3步骤的求梯度顺序和对多个梯度值的累加规则恰好是求导链式法则的程序表述）

正因为求导链式法则衍生的梯度累加规则，张量的grad梯度不会自动清零，在需要的时候需要手动置零。

叶子节点和非叶子节点

执行上述代码，我们会发现loss.grad并不是我们期望的1，而是None。类似地 y1.grad 以及 y2.grad也是 None。

这是由于它们不是叶子节点张量。

在反向传播过程中，只有 is_leaf=True 的叶子节点，需要求导的张量的导数结果才会被最后保留下来。

那么什么是叶子节点张量呢？叶子节点张量需要满足两个条件。

1，叶子节点张量是由用户直接创建的张量，而非由某个Function通过计算得到的张量。

2，叶子节点张量的 requires_grad属性必须为True.

Pytorch设计这样的规则主要是为了节约内存或者显存空间，因为几乎所有的时候，用户只会关心他自己直接创建的张量的梯度。

所有依赖于叶子节点张量的张量, 其requires_grad 属性必定是True的，但其梯度值只在计算过程中被用到，不会最终存储到grad属性中。

如果需要保留中间计算结果的梯度到grad属性中，可以使用 retain_grad方法。 如果仅仅是为了调试代码查看梯度值，可以利用register_hook打印日志。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import torch
x = torch.tensor(3.0,requires_grad=True)
y1 = x + 1
y2 = 2*x
loss = (y1-y2)**2

loss.backward()
print("loss.grad:", loss.grad) # loss.grad: None
print("y1.grad:", y1.grad)	# y1.grad: None
print("y2.grad:", y2.grad)	# y2.grad: None
print(x.grad)	# tensor(4.)

print(x.is_leaf) # True
print(y1.is_leaf) # False
print(y2.is_leaf) # False
print(loss.is_leaf)	# False

利用retain_grad可以保留非叶子节点的梯度值，利用register_hook可以查看非叶子节点的梯度值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import torch 

#正向传播
x = torch.tensor(3.0,requires_grad=True)
y1 = x + 1
y2 = 2*x
loss = (y1-y2)**2

#非叶子节点梯度显示控制
y1.register_hook(lambda grad: print('y1 grad: ', grad))	# y2 grad:  tensor(4.)
y2.register_hook(lambda grad: print('y2 grad: ', grad))	# y1 grad:  tensor(-4.)
loss.retain_grad()	

#反向传播
loss.backward()
print("loss.grad:", loss.grad)	# loss.grad: tensor(1.)
print("x.grad:", x.grad)	 # loss.grad: tensor(1.)

计算图在TensorBoard中的可视化

可以利用 torch.utils.tensorboard 将计算图导出到 TensorBoard进行可视化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from torch import nn 
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.w = nn.Parameter(torch.randn(2,1))
        self.b = nn.Parameter(torch.zeros(1,1))

    def forward(self, x):
        y = x@self.w + self.b
        return y

net = Net()

from torch.utils.tensorboard import SummaryWriter
writer = SummaryWriter('./data/tensorboard')
writer.add_graph(net,input_to_model = torch.rand(10,2))
writer.close()

%load_ext tensorboard
#%tensorboard --logdir ./data/tensorboard

from tensorboard import notebook
notebook.list() 

#在tensorboard中查看模型
notebook.start("--logdir ./data/tensorboard")

img

pytorch的层次结构

5个不同的层次结构：即硬件层，内核层，低阶API，中阶API，高阶API [torchkeras]

Pytorch的层次结构从低到高可以分成如下五层。

最底层为硬件层，Pytorch支持CPU、GPU加入计算资源池。

第二层为C++实现的内核。

第三层为Python实现的操作符，提供了封装C++内核的低级API指令，主要包括各种张量操作算子、自动微分、变量管理. 如torch.tensor,torch.cat,torch.autograd.grad,nn.Module. 如果把模型比作一个房子，那么第三层API就是【模型之砖】。

第四层为Python实现的模型组件，对低级API进行了函数封装，主要包括各种模型层，损失函数，优化器，数据管道等等。 如torch.nn.Linear,torch.nn.BCE,torch.optim.Adam,torch.utils.data.DataLoader. 如果把模型比作一个房子，那么第四层API就是【模型之墙】。

第五层为Python实现的模型接口。Pytorch没有官方的高阶API。为了便于训练模型，博客作者仿照keras中的模型接口，使用了不到300行代码，封装了Pytorch的高阶模型接口torchkeras.Model。如果把模型比作一个房子，那么第五层API就是模型本身，即【模型之屋】。

低阶API示范

下面的范例使用Pytorch的低阶API实现线性回归模型和DNN二分类模型

低阶API主要包括张量操作，计算图和自动微分。

1
2
3
4
5
6
7
8
9
10
import os
import datetime

#打印时间
def printbar():
    nowtime = datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S')
    print("\n"+"=========="*8 + "%s"%nowtime)

# mac系统上pytorch和matplotlib在jupyter中同时跑需要更改环境变量
# os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE"
一、线性回归模型
  1. data prepare
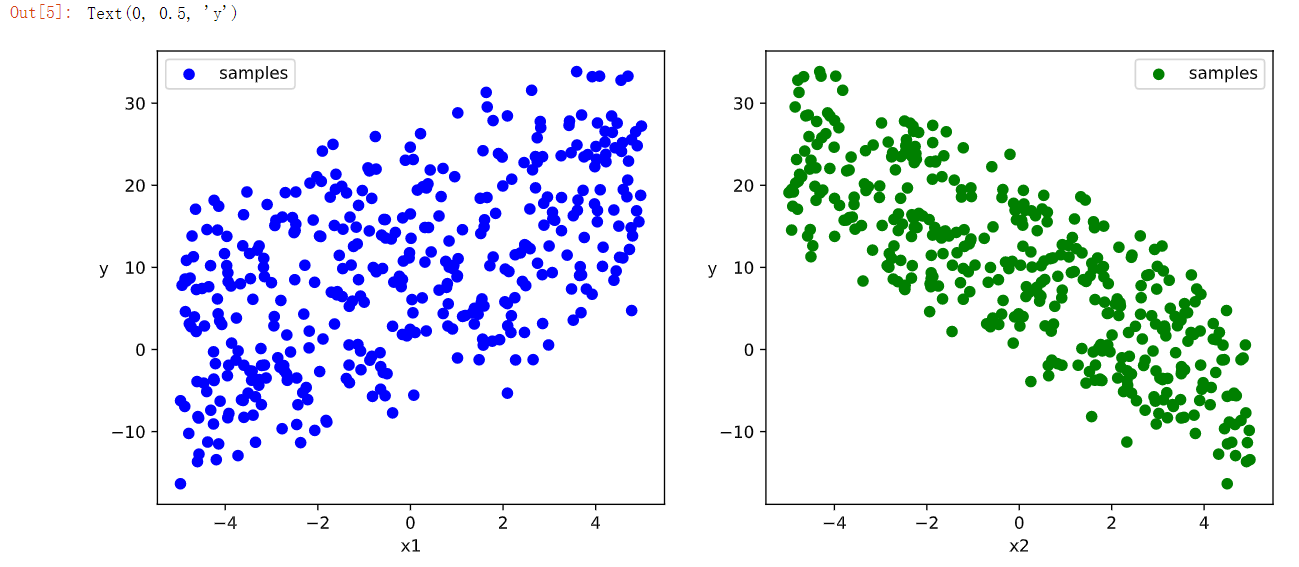
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import numpy as np 
import pandas as pd
from matplotlib import pyplot as plt 
import torch
from torch import nn


#样本数量
n = 400

# 生成测试用数据集
X = 10*torch.rand([n,2])-5.0  #torch.rand是均匀分布 
w0 = torch.tensor([[2.0],[-3.0]])
b0 = torch.tensor([[10.0]])
Y = X@w0 + b0 + torch.normal( 0.0,2.0,size = [n,1])  # @表示矩阵乘法,增加正态扰动
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 数据可视化

%matplotlib inline
%config InlineBackend.figure_format = 'svg'

plt.figure(figsize = (12,5))  # 图形窗口的宽度为 12 英寸，高度为 5 英寸
ax1 = plt.subplot(121)
#画散点图 
ax1.scatter(X[:,0].numpy(),Y[:,0].numpy(), c = "b",label = "samples")
#设置图例
ax1.legend()  # 没有此不会有samples图例
plt.xlabel("x1")
plt.ylabel("y",rotation = 0)

ax2 = plt.subplot(122)
ax2.scatter(X[:,1].numpy(),Y[:,0].numpy(), c = "g",label = "samples")
ax2.legend()
plt.xlabel("x2")
plt.ylabel("y",rotation = 0)

image-20230119174857563

注：**plt.subplot(121) 是 matplotlib 库中用于创建多个子图的函数之一。其中，121 是参数，表示将整个图分成 1 行 2 列，并在第 1 个位置创建子图。因此，这条语句将创建一个 1 行 2 列的子图网格，并在第一个子图中绘制图形。**

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 构建数据管道迭代器
def data_iter(features, labels, batch_size=8):
    num_examples = len(features)
    indices = list(range(num_examples))
    np.random.shuffle(indices)  #样本的读取顺序是随机的
    for i in range(0, num_examples, batch_size):
        indexs = torch.LongTensor(indices[i: min(i + batch_size, num_examples)])
        yield  features.index_select(0, indexs), labels.index_select(0, indexs)

# 测试数据管道效果   
batch_size = 8
(features,labels) = next(data_iter(X,Y,batch_size))
print(features)
print(labels)

'''
tensor([[ 1.0449, -0.3581],
        [-3.0645, -2.9230],
        [ 3.7969, -4.5846],
        [-0.2429,  0.5349],
        [ 2.2708,  0.1713],
        [ 4.6910,  4.3684],
        [ 2.1360, -4.7411],
        [ 3.3687,  0.3648]])
tensor([[15.6397],
        [14.1632],
        [31.6240],
        [ 7.4723],
        [11.8881],
        [ 6.8064],
        [30.4618],
        [15.2579]])
'''
  1. define the model
1
2
3
4
5
6
7
8
9
10
11
12
13
# 定义模型
class LinearRegression: 
    def __init__(self):
        self.w = torch.randn_like(w0,requires_grad=True)
        self.b = torch.zeros_like(b0,requires_grad=True)
    #正向传播
    def forward(self,x): 
        return x@self.w + self.b
    # 损失函数
    def loss_func(self,y_pred,y_true):  
        return torch.mean((y_pred - y_true)**2/2)

model = LinearRegression()
  1. model training
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def train_step(model, features, labels):
    predictions = model.forward(features)
    loss = model.loss_func(predictions,labels)
    # 反向传播求梯度
    loss.backward()
    
    # 使用torch.no_grad()避免梯度记录，也可以通过操作 model.w.data 实现避免梯度记录 
    with torch.no_grad():
        # 梯度下降法更新参数
        model.w -= 0.001*model.w.grad
        model.b -= 0.001*model.b.grad
        # 梯度清零
        model.w.grad.zero_()
        model.b.grad.zero_()
    return loss
1
2
3
4
# 测试train_step效果
batch_size = 10
(features,labels) = next(data_iter(X,Y,batch_size))
train_step(model,features,labels)

Out[]: tensor(141.2280, grad_fn=)

1
2
3
4
5
6
7
8
9
10
11
12
def train_model(model,epochs):
    for epoch in range(1,epochs+1):
        for features, labels in data_iter(X,Y,10):
            loss = train_step(model,features,labels)

        if epoch%200==0:
            printbar()
            print("epoch =",epoch,"loss = ",loss.item())
            print("model.w =",model.w.data)
            print("model.b =",model.b.data)

train_model(model,epochs = 1000)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
================================================================================2023-01-20 17:03:37
epoch = 200 loss =  2.0936481952667236
model.w = tensor([[ 2.0185],
        [-2.9519]])
model.b = tensor([[10.0203]])

================================================================================2023-01-20 17:03:38
epoch = 400 loss =  1.3962600231170654
model.w = tensor([[ 2.0212],
        [-2.9512]])
model.b = tensor([[10.0241]])

================================================================================2023-01-20 17:03:39
epoch = 600 loss =  0.3997553586959839
model.w = tensor([[ 2.0167],
        [-2.9528]])
model.b = tensor([[10.0237]])

================================================================================2023-01-20 17:03:41
epoch = 800 loss =  1.8717002868652344
model.w = tensor([[ 2.0194],
        [-2.9495]])
model.b = tensor([[10.0240]])

================================================================================2023-01-20 17:03:42
epoch = 1000 loss =  1.8542640209197998
model.w = tensor([[ 2.0176],
        [-2.9507]])
model.b = tensor([[10.0237]])
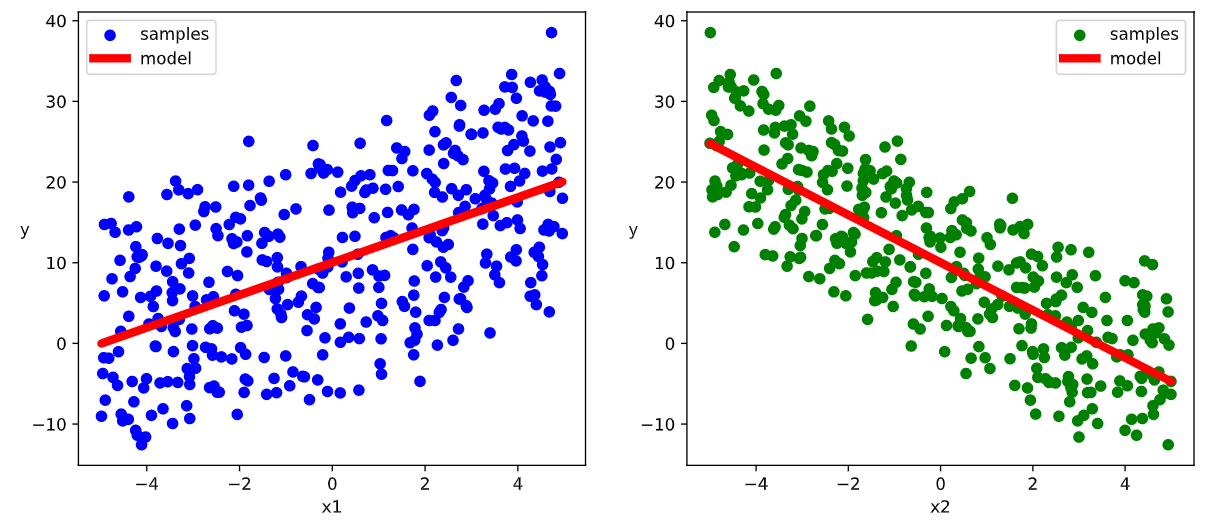
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 结果可视化
%matplotlib inline

plt.figure(figsize = (12,5))
ax1 = plt.subplot(121)
ax1.scatter(X[:,0].numpy(),Y[:,0].numpy(), c = "b",label = "samples")
ax1.plot(X[:,0].numpy(),(model.w[0].data*X[:,0]+model.b[0].data).numpy(),"-r",linewidth = 5.0,label = "model")
ax1.legend()
plt.xlabel("x1")
plt.ylabel("y",rotation = 0)


ax2 = plt.subplot(122)
ax2.scatter(X[:,1].numpy(),Y[:,0].numpy(), c = "g",label = "samples")
ax2.plot(X[:,1].numpy(),(model.w[1].data*X[:,1]+model.b[0].data).numpy(),"-r",linewidth = 5.0,label = "model")
ax2.legend()
plt.xlabel("x2")
plt.ylabel("y",rotation = 0)

plt.show()

image-20230120170539911

二、DNN二分类模型
  1. data prepare
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import numpy as np 
import pandas as pd 
from matplotlib import pyplot as plt
import torch
from torch import nn
%matplotlib inline
%config InlineBackend.figure_format = 'svg'

#正负样本数量
n_positive,n_negative = 2000,2000

#生成正样本, 小圆环分布
r_p = 5.0 + torch.normal(0.0,1.0,size = [n_positive,1]) 
theta_p = 2*np.pi*torch.rand([n_positive,1])
Xp = torch.cat([r_p*torch.cos(theta_p),r_p*torch.sin(theta_p)],axis = 1)
Yp = torch.ones_like(r_p)

#生成负样本, 大圆环分布
r_n = 8.0 + torch.normal(0.0,1.0,size = [n_negative,1]) 
theta_n = 2*np.pi*torch.rand([n_negative,1])
Xn = torch.cat([r_n*torch.cos(theta_n),r_n*torch.sin(theta_n)],axis = 1)
Yn = torch.zeros_like(r_n)

#汇总样本
X = torch.cat([Xp,Xn],axis = 0)
Y = torch.cat([Yp,Yn],axis = 0)


#可视化
plt.figure(figsize = (6,6))
plt.scatter(Xp[:,0].numpy(),Xp[:,1].numpy(),c = "r")
plt.scatter(Xn[:,0].numpy(),Xn[:,1].numpy(),c = "g")
plt.legend(["positive","negative"])

img