深度学习的不确定性和校准

几个概念

不确定性是什么

  • 偶然事件不确定性

    数据生成本身具有的随机性，无法通过收集更多数据来消除不确定（应该优化采集数据的策略）

  • 认知不确定性

    就是模型的不确定性， 模型对输入数据因为训练的各种问题导致的不准确，与某一单一的数据无关

  • 超出分布的不确定性

    就是常说的 OOD(out of distribution)问题, 感觉模型学习就是一个记忆的过程，遇到分布之外的数据模型就会胡说八道，这就涉及到了异常检测

    假设数据集 A(报纸上的文本数据)，B(维基百科上的文本数据)，利用 A 训练一个模型，然后利用 A，B 分别作为输入去做测试，此时 A 就是域内数据 in-domain，B 叫 out-domain，而 open-domain 就更加广泛随意了，例如将 AB 混合起来成为数据集 C，C 去用作模型的测试输入，这时 C 就是 open-domain。

置信度是什么

简单来说就是 对决策的信心程度，具体到模型里，logits 就能反应置信度

复习: 概率论/机器学习中的置信度和置信区间

置信度就是对事件的估计的信心，置信区间则是一个范围，在固定置信度下估计某个参数或事件落在的区间

参数估计：利用总体抽样得到的信息来估计总体的某些参数或参数的某些函数

  1. 点估计

    • 矩估计 用样本矩估计总体矩 依据是大数定理
    • 最大似然估计 找出概率的最大值

  2. 区间估计

    img

各种假设检验方法（如 t 检验）：可以推断若在测试集上观察到学习器A优于B,则A的泛化性能是否在统计意义上优于B,以及这个结论的把握有多大

概率型模型评估指标：

  1. 布里尔分数（Brier Score）：

概率预测相对于测试样本的均方误差，衡量了概率距离真实标签结果的差异：

$Brier Score=(p−o)^2$

  1. 对数似然函数 Log Loss (二元交叉熵损失)

    对数似然函数的取值越小，则证明概率估计越准确，模型越理想

$Log Loss=−(y⋅log(p)+(1−y)⋅log(1−p))$

  1. 可靠性曲线 （校准曲线）

是用于评估分类模型的概率预测准确性的一种图形化工具。它帮助我们了解模型的概率预测与实际观测之间的关系，以便判断模型是否具有良好的概率校准性。

在分类问题中，模型不仅会做出类别预测，还会给出属于每个类别的概率估计。这些概率估计可以被视为模型对于样本属于不同类别的自信程度。而良好的概率校准性意味着，模型预测的概率与实际发生的频率相匹配。

可靠性曲线通常是一个散点图，其中 x 轴表示模型预测的概率，y 轴表示实际观测的频率（即在给定预测概率范围内的实际样本比例）。理想情况下，如果模型的概率预测是完全校准的，那么这些点将会在对角线 y = x 上。这表示当模型预测的概率为 p 时，实际观测的频率也应该接近 p。

然而，在实际应用中，模型可能会存在概率校准性不足的情况。例如，模型可能倾向于给出过于极端的概率预测，导致可靠性曲线上的点偏离了对角线。通过观察可靠性曲线，我们可以判断模型是否需要进行概率校准，以提高其概率预测的准确性。

image-20230829205256146

  • 逻辑回归是一种特殊情况，因为它在设计上经过了良好的校准，因为它的目标函数最小化了对数损失函数
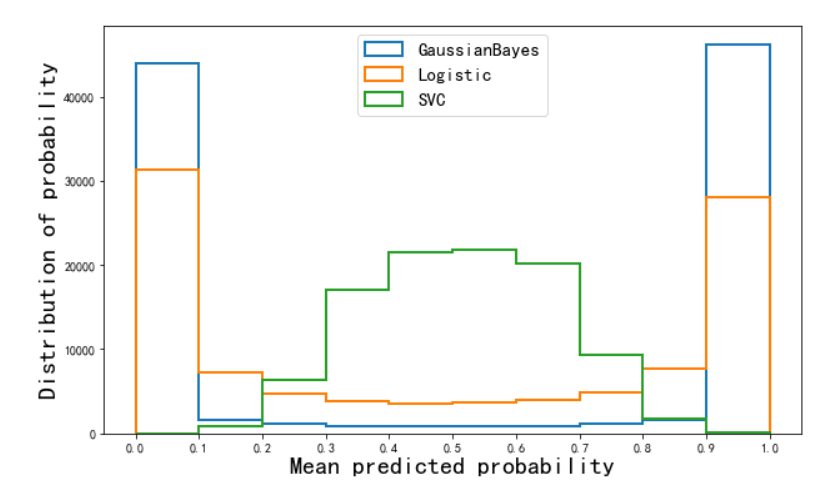
  1. 预测概率的直方图

预测概率的直方图是一种图表，用于显示分类模型对于不同类别的概率预测的分布情况。它可以帮助我们理解模型对于不同类别的预测置信程度分布，从而了解模型的概率预测性能和可靠性。

在一个分类问题中，模型通常会输出每个样本属于不同类别的概率估计值。例如，在二分类问题中，模型会给出样本属于正类别的概率 p，以及属于负类别的概率 1 − p。预测概率的直方图将按照这些概率值的范围，将预测概率划分为不同的区间，并统计落在每个区间内的样本数量。

直方图的 x 轴通常表示概率的范围（例如从 0 到 1），y 轴表示落在对应概率区间内的样本数量。通过观察直方图，我们可以获得以下信息：

  1. 概率分布： 我们可以看到模型的概率预测在不同区间的分布情况。这有助于了解模型是如何对于不同类别的概率进行预测的。
  2. 置信程度： 预测概率的直方图可以显示出模型的置信程度分布。高度集中的直方柱表示模型对于概率的估计比较自信，而分散的分布可能表示模型对于预测的不确定性较大。
  3. 校准性： 如果模型的概率预测是校准的，那么直方图应该在每个区间内都大致匹配实际观测的频率分布。

预测概率的直方图通常用于了解模型的概率预测性能和分布情况，但它并不直接提供关于模型分类准确性的信息。为了更全面地评估模型，可以结合其他工具如可靠性曲线、Brier 分数等进行分析。

image-20230829205530721

不确定性估计 uncertainty estimates

就是计算 置信度 和 真实准确率 之间的误差程度，得到不确定性的概率值 uncertainty，实际上 uncertainty 同样也反映置信度

关注模型对预测结果有多大的把握，从而为模型排除错误

calibration

评价指标：

  1. ECE-预期校准误差

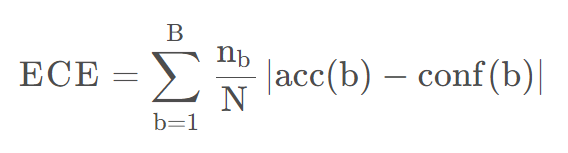
    image-20230830154848108

    ECE 是基于可靠性图来的

    soft ECE:

    Soft-Binned ECE = $$\sum_{i=1}^n \frac{w_i}{\sum_{j=1}^n w_j} |a_i - c_i|$$

    其中，n 是分区的数量，w i 是第 i 个分区的权重，a i 是第 i 个分区内的预测概率的平均值，c i 是第 i 个分区内的真实概率的平均值。Soft-Binned ECE 的关键点是使用一个连续的函数来计算每个分区的权重和平均值，而不是使用一个离散的函数。具体来说，对于每个样本(x, y)，它的预测概率为 p = f(x)，它对应的分区索引为 k = ⌊ n p ⌋+1，那么它对第 i 个分区的权重贡献为：

    $w_i(x,y)=max(0,1−∣i−k∣)$

    它对第 i* 个分区的平均预测概率贡献为：

    $a_i(x,y)=w_i(x,y)p$

    它对第 i* 个分区的平均真实概率贡献为：

    $c_i(x,y)=w_i(x,y)I[y=argmax(p)]$

    其中 I 是指示函数。可以看出，这些函数都是连续可微的，因此可以直接用于训练过程中。更多细节可以参考 这篇论文。

    Region ECE：把样本分 Region

  2. MCE-最大校准误差

（Expected Calibration Error）

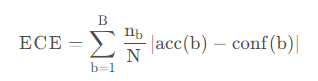
image-20230718151732832

image-20230721204209858

其中，b 代表第 b 个 bin，B 代表 bin 的总数，$n_b$ 代表第 b 个 bin 中样本的总数，acc(b)代表第 b 个 bin 中样本真实标签的平均值，conf(b)代表第 b 个 bin 中模型预测概率的平均值。两者之差的绝对值就能度量模型的置信度，差距越大代表模型置信度越小。

衡量了置信度分数与基本事实的不确定性之间的一致性

  1. Negative log likelihood 负对数似然

image-20230830145609133

  1. Reliability Diagrams 可靠性曲线

  2. AvUC

    Soft AvUC 是基于 AvUC (Average Uncertainty Calibration) 的改进，AvUC 是一种校准误差度量，它将预测概率分成若干个区间（bin），然后计算每个区间内预测概率的方差和真实概率的方差之间的差异，再对所有区间求加权平均。Soft AvUC 的主要创新是将分区操作从离散化变为连续化，这样可以使得训练目标可微分(可用来直接训练)，并且可以避免分区数量和位置的选择对结果的影响。

    Soft AvUC 的具体公式如下：

    Soft AvUC = $$\sum_{i=1}^n \frac{w_i}{\sum_{j=1}^n w_j} |v_i - u_i|$$

  3. AUROC

接收器操作特征曲线下的面积（AUROC, ROC）评估置信度分数在 区分正确和错误样本方面的能力

  1. AUPRC

精度-召回曲线下的面积（AUPRC）衡量识别正确样本（AUPRC-Positive, PR-P）和 错误样本（AUPRC-Negative, PR-N）的能力

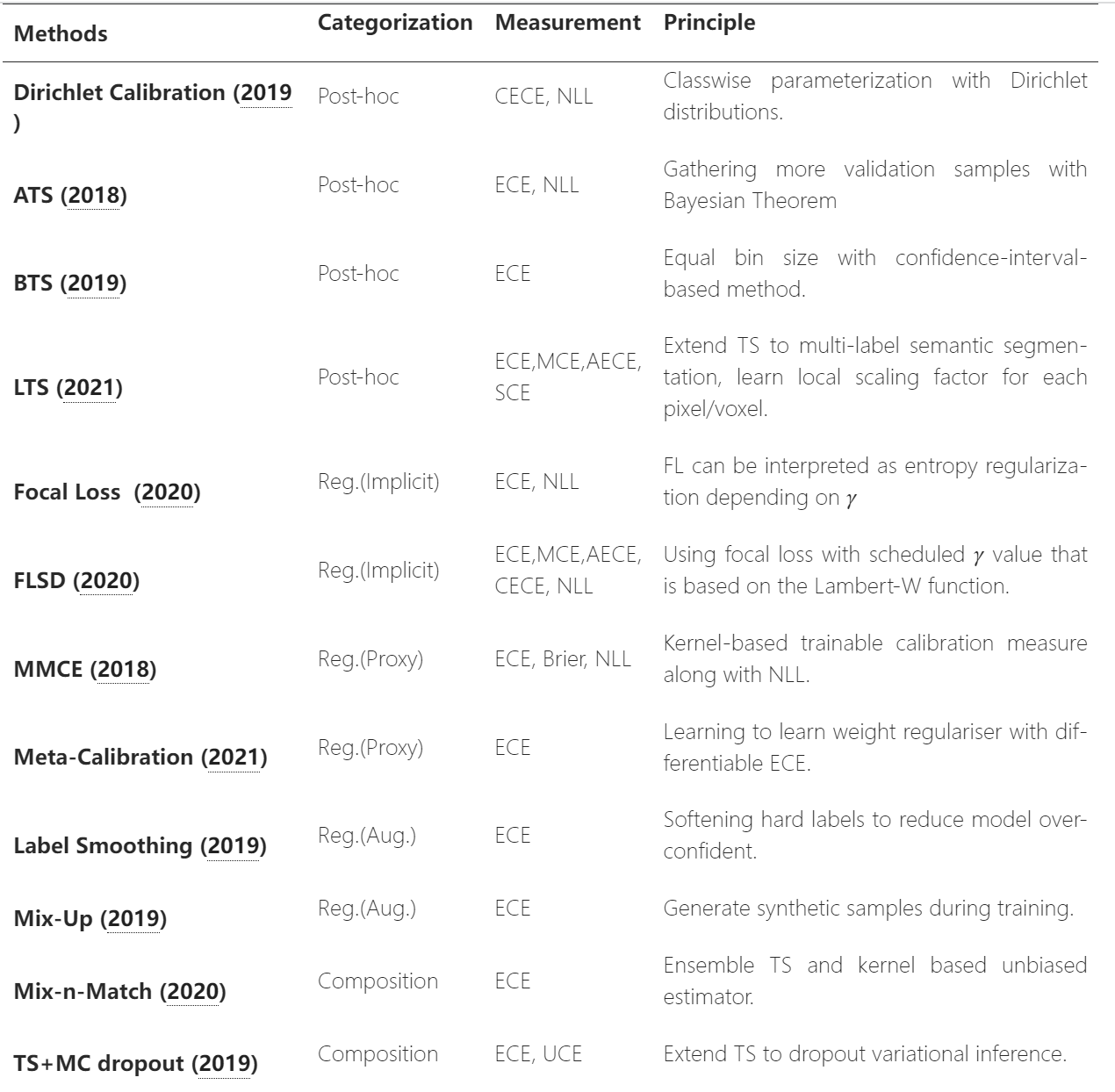
校准方法

Calibration in Deep Learning: A Survey of the State-of-the-Art

分类：

  • 先验校准(prior calibration)、后验校准(post calibration)

  • 参数化方法、 非参数化方法（通过直方图分箱结果来校准）

    参数化方法假设校准映射属于有限维参数化族族，可以通过最小化损失函数来学习参数。非参数化方法则假设校准映射由无限维参数描述，可以通过直方图、贝叶斯平均或保序回归等方法进行学习。

https://aitechtogether.com/article/28062.html

  1. 先验校准：

    • 数据增强

    • few shot

    • COT

    • Deep Ensemble

      模型集成

      • 在模型训练之前，Deep Ensemble需要选择合适的神经网络结构和参数，以及集成的数量和方式。这些选择会影响模型的复杂度和多样性，从而影响模型的泛化能力和稳定性。
      • 在模型训练过程中，Deep Ensemble需要对不同的神经网络进行随机初始化和训练，以及对它们的输出进行平均或统计。这些操作会影响模型的学习过程和预测结果，从而影响模型的准确性和不确定性。

    • 魔改损失函数 （正则化操作）

      不良校准与负对数似然 (NLL) 的过度拟合有关

      • dice 损失代码：https://blog.csdn.net/hqllqh/article/details/112056385

      • LogitNorm 交叉熵损失：https://arxiv.org/abs/2205.09310

        对传统交叉熵的改进，主要解决神经网络过拟合和模型矫正问题。虽然实验都是在 OOD 检测任务上做的，但是这个方法应该是具有比较强的通用性的，适用于一些需要知识迁移的任务。本文通过理论推导结合实验分析的方式，逐步引出方法，这个行文思路值得借鉴

      • [On/Off-manifold regularization](On/Off-manifold regularization) 损失函数上加正则项

      • Distance-based logits & One vs ALL: https://arxiv.org/abs/2007.05134

      DM: logits zj 被定义为嵌入和最后c一层的权重之间的负欧氏距离，即 zj = − kf θ(x) − wjk

      image-20230725170352955

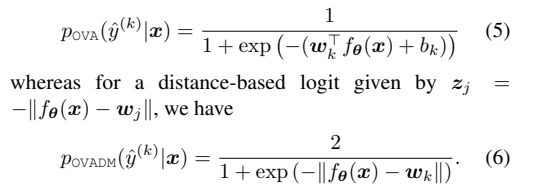
      One vs ALL: image-20230725170426142

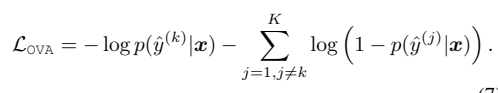
      image-20230725170446060

      其中使用平滑算法

      trick:

      平滑算法在transformer中softmax改进的应用：

      $W_{i,j} = \frac{\exp(\text{score}(q_i, k_j))}{\sum_{j=1}^{m} \exp(\text{score}(q_i, k_j)) + \exp(\text{extra_logit})}$

      插眼：半监督、伪标签、熵正则化

  2. 后验校准

    • platt 方法使用训练、校准和测试分割来校准分类器（adaboost）

      1
      2
      3
      4
      5
      6
      7
      8
      # uncalibrated model
      clf = AdaBoostClassifier(n_estimators=50)
      y_proba = clf.fit(X_train, y_train).predict_proba(X_test)
      # calibrated model
      calibrator = LogisticRegression()
      calibrator.fit(clf.predict_proba(X_calib), y_calib)

      y_proba_calib = calibrator.predict_proba(y_proba)

      使用校准分类器

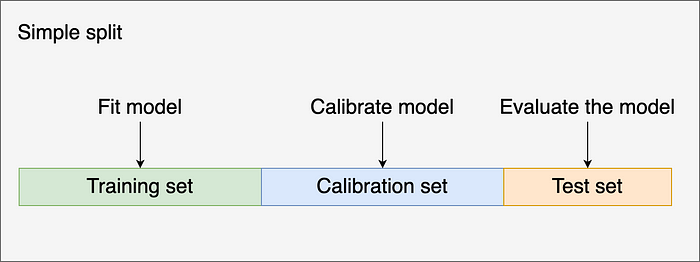      img train cali test分开

    • Isotonic Regression 等保回归 –让输出保持单调性

      将一组无序的数变为有序，一组数为 {1，3，2，2} ，遍历发现3>2，将这两个数转为均值，即 {1,2.5,2.5,2}，然后又发现2.5>2，于是将3,2,2转为三者的均值，即 {1,2.5,2.5,2.5}
      为了保证不引入偏差，用作校准的数据集应该和训练模型的数据集不同。

    • 温度缩放 T scaling

      对logits进行缩放

      img

      要注意的是，上述方法需要在 validation set 上进行优化，来学习参数 temperature，而不能在 training set 上进行学习，所以 Temperature scaling 是一个 post process，即后处理步骤，这种方法也暂时只能用于分类任务，不能用于回归。

      补充:

      NRTP(Neural Rank-Preserving Transforms):

      将温度缩放改进：让每个样本有自己的温度参数T(x),而不是全局的T。公式为: fTθ(zb;x) = zb/Tθ(x)

      作者观察到温度缩放保持logits排序的关键性质是单调性。因此,作者提出使用更一般的单调校准器:

      fθ(zb;x) = [gθ(zb1;x),…,gθ(zbK;x)]

      其中gθ单调递增。这保持了排序关系所以也保持了精确度。

      使用单调的两层网络实现

      作者使用了一种两层网络结构来学习单调的gθ函数:

      gθ(zi;x) = Σj ajφ((zi - bθj(x))/Tθj(x))

      其中aj≥0,Tθj(x)>0,φ是单调的非线性激活函数。这可以保证单调性。

      Region-dependent temperature scaling

      同样的改进temperature、分区域不同t的温度缩放

    • MC(蒙特卡洛)-Dropout

      在inference中也使用Dropout、对于一个样本的 inference，MC-Dropout 要求随机进行 K 次 dropout，进行 K 次前传，得到 K 个输出结果。而 K 个输出结果再进行 ensemble

      image-20230914145040644

      其他论文（大模型）

      1. Teaching models to express their uncertainty in words 口头表达的置信度（用语言文本直接微调 confidence

      2. Large Language Models Are Reasoning Teachers

        一种蒸馏的方式，大模型的输出来微调小模型

      3. Can LLMs Express Their Uncertainty? An Empirical Evaluation of Confidence Elicitation in LLMs

        有两个指标可用于衡量模型的不确定性：模型生成的文本输出以及对同一问题的多次回答之间的一致性

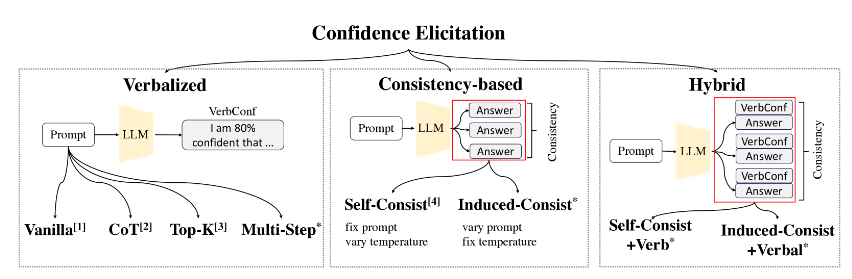
        image-20230831235327273

        ​ 可靠的不确定性估计对于人机协作至关重要，可以促进更加理性和明智的决策。具体而言，准确获得模型的置信度可以为其响应的可靠性提供有价值的洞察，促进风险评估和错误缓解，并减少自然语言生成任务中的错觉。

        ​ 以前的 model 获得置信度主要依赖 model logit 及其相关校准技术。校准是指将模型的预测结果调整为更接近真实概率的方法，使得模型的置信度能够更准确地反映实际概率。常用的校准技术包括 平滑方法、温度缩放、直方图校准 等。

        ​ 然而对于 LLMs, 使用 model logits 有很多限制，一、对数几率在许多情况意味着过度自信（见 paper1）；二、logits 仅捕捉模型对下一个 token 的不确定性，而不提供对特定主张可靠性的评估，而人类式回答中期望的是能够评估 主张本身的可靠性。例如，在生成报告时，模型明确指示其断言的可靠性非常重要，这不能直接通过标记的 logits 实现。三、封源 LLMs 其商业化 API 仅允许文本输入和输出，缺乏 model logits 和 embeddings。因此，这些局限性需要对 LLMs 进行 non-logit-based 方法的不确定性 eclicitation，即 confidence elicitation。

        ​ 本文目标：1）探索不需要模型微调或访问专有信息的置信度唤起方法；2）对它们的表现进行比较分析，以揭示可以提供更准确的不确定性估计（即置信度）的方法和方向。

        ​ 此文混合了 COT 和 Consistency实现了更好的校准

        image-20230921193858057

        $$Confidence=\sigma(W_1\cdot LCE + W_2\cdot NLCE + b)$$

        LCE如果本身很低的话，说明总有些词的预测概率本来就低，整体也不一定可信；然后再加上NLCE的判定结合（NLCE有点道理就是，大模型肯定倾向于自己的答案，所以口头输出的置信度一般都会大于50%，所以当能判别其答案错误时就调低置信度）

      4. Making Pre-trained Language Models both Task-solvers and Self-calibrators

        无监督训练置信度

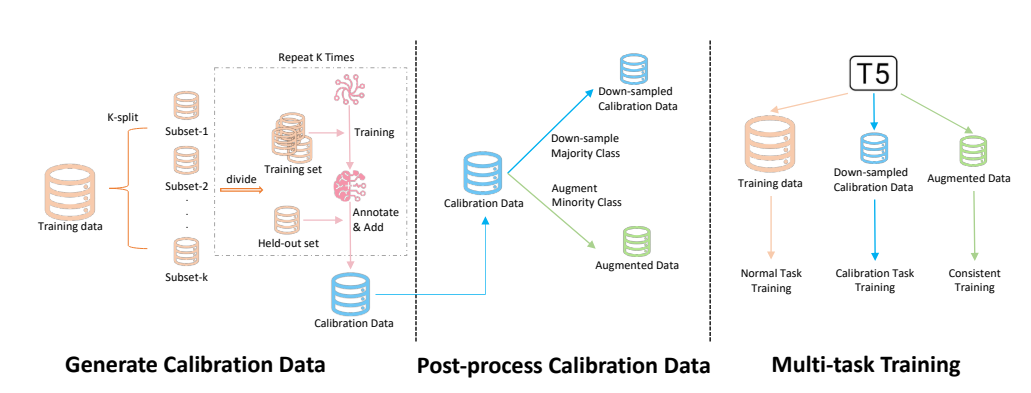
        image-20230721140312656

        ​ 在实践中，我们需要有效地利用原始任务和校准任务的训练样本。提出了三个挑战： - 有限的训练样本：如何有效地利用训练样本来提高校准任务性能，同时保持原始任务性能？ - 数据不平衡：由于 PLMs 具有较高的性能，正样本（被正确分类的样本）在校准训练集中占据显著地位，导致数据不平衡问题。 - 分布偏移：在部署时，PLMs 也需要展示对于分布外（OOD）样本的鲁棒性，给出合理的置信度分数。

        ​ 实验的三种基准方法：（1）Vanilla：将原始预测概率作为置信度估计；（2）温度缩放（TS）：应用温度缩放方法来校准 PLMs 的置信度得分；（3）标签平滑（LS）：应用标签平滑来防止 PLMs 对其预测过于自信

        补充：半监督学习：

        https://zhuanlan.zhihu.com/p/387907614

        PI Model(一个半监督模型的框架)

        img

      5. Thrust: Adaptively Propels Large Language Models with External Knowledge

        工作流程：

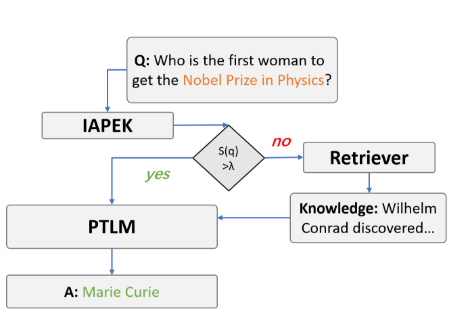
        image-20230721131558174

        有跟我自己做的 arxiv 检索那个有相关，查到的信息一个是不一定准确，一个是不一定有用，可能有很大噪声

        提出了 the Instance-level Adaptive Propulsion of External Knowledge（IAPEK）模块 （which adaptively retrieves external knowledge when it is necessary.）

        给出了 Trust 的置信度估计模块

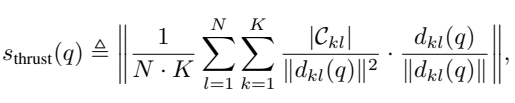
        image-20230721135338307

        s(q)就是 trust 打分函数

        设计原则：注意，等式 1 中ℓ 2 范数内的表达式可以视为从查询向量 f(q)指向质心向量{mkl}的规范化（单位）向量{dkl(q)/∥ dkl(q)∥}的加权平均值。权重与聚类大小成正比，与查询和质心之间的平方距离成反比。这样的设计选择基于早期关于知识的表示假设得出的以下原则。首先，当一个任务的样本被良好聚类，并且如果 q 接近其中一个聚类而远离其他聚类，意味着查询实例 q 可以通过 PTLM 的内在知识得到很好地解决，Thrust 评分应该较高。假设 mkl 是 q 靠近的聚类质心，那么我们观察到等式 1 中分母中对应的∥ dkl ∥ 2 项会使得对应的项在计算中占主导地位，并且值较大。其次，如果 q 远离所有的聚类质心，即查询超出了 PTLM 的知识范围，那么二次项∥ dkl ∥ 2 将迅速抑制等式 1 中的所有项，使得 Thrust 评分消失。第三，当 PTLM 不能在其隐藏状态中足够地对任务样本进行聚类时，这意味着 PTLM 没有足够的知识来解决整个任务。在这种情况下，单位向量 dkl(q)/∥ dkl(q)∥将随机指向不同的方向，使得等式 1 中ℓ 2 范数内的平均向量减小。最后，我们首先将每个类别中的样本聚合成 K 个簇，然后再计算 Thrust 评分，主要原因是即使属于同一类别，它们仍然可能分布在多个簇中。等式 1 中的|Ckl|项用于加重指向更大簇的矢量 dkl(q)/∥ dkl(q)∥。然而，我们发现 K 可以相对较小。

      6. Calibration, Entropy Rates, and Memory in Language Models

        发现了在各种语料库上训练的最先进语言模型中熵放大的普遍现象。基于这一发现，本文的重点有两个方面：一是基于模型长期属性（例如熵率）的任何测量不匹配来改进生成，并提供可证明的保证；二是量化模型预测与远期过去的依赖关系。这两个方面的核心是基于校准的方法，这种方法在统计学和机器学习的其他领域中被使用

        补充：KL 散度（Kullback–Leibler divergence，缩写 KLD）是一种统计学度量，表示的是一个概率分布相对于另一个概率分布的差异程度，在信息论中又称为 相对熵（Relative entropy）。

        ​ 设离散概率空间 X 上有两个概率分布 P 和 Q, 那么 P 相对于 Q 的 KL 散度定义如下：

      ​ $D_{K L}(P | Q)=\sum_{x \in X} P(x) \ln \left(\frac{P(x)}{Q(x)}\right)=\sum_{x \in X} P(x)(\ln (P(x))-\ln (Q(x))) \text {. }$
      ​ 对于连续型随机变量，设概率空间 X 上有两个概率分布 P 和 Q, 其概率密度分别为 p 和 q, 那么，P 相对于 Q 的 KL 散度定义如下：

      ​ $D_{K L}(P | Q)=\int_{-\infty}^{+\infty} p(x) \ln \left(\frac{p(x)}{q(x)}\right) d x$

      ​ 显然，当 P = Q 时，DKL = 0。
      ​ 根据 KL 散度的定义，可以知道此度量是没有对称性的。也就是说，P 相对于 Q 和 KL 散度一般并不等于 Q 相对
      于 P 的。由于 K 工散度能够衡量两个概率分布之间的差异，现在广泛用于机器学习中，用于评估生成模型所产生的数据
      分布与实际数据分布之间的差异程度。

多分类数据不平衡

也会导致overconfidence

解决：

  • 数据级方法

    此方案处于与分类器无关的预处理阶段

    1. SMOTE(利用knn线性内插生成少样本, 同时减少多样本) 和 DeepSMOTE（使用生成对抗网络（GANs）来生成更逼真的合成样本）

  • 算法级方法

    修改网络和模型的权重、cost-sensitive等

  • Ensemble

    模型集成

    Loss Function:

在自然语言处理（NLP）中，二进制交叉熵（BCE）损失常用于多标签文本分类（Bengio et al., 2013）。给定一个包含N个训练实例的数据集，每个实例具有一个多标签的真实标签（其中C是类别的数量），以及分类器的输出概率P(y_i)，BCE损失可以定义如下（为简单起见，平均减少步骤未显示出来）：

$BCE = -1/N * Σ [Σ (y_i * log(P(y_i)) + (1 - y_i) * log(1 - P(y_i)))]$

 通常情况下，纯粹的BCE损失函数容易受到头部类别或负实例的支配而产生标签不平衡的问题（Durand et al., 2019）。以下，我们描述了三种解决多标签文本分类中长尾数据集类别不平衡问题的替代方法。这些平衡方法的主要思想是重新加权BCE，以便罕见的实例-标签组合能够直观地获得合理的“关注”。
   
 令![image-20230906164649369](C:\Users\97854\AppData\Roaming\Typora\typora-user-images\image-20230906164649369.png)

 交叉熵损失可写为

 $LOSS_{ce} = -log(p_t)$

 1. Focal loss (FL) 	（Lin et al., 2017）

 ![image-20230906163115279](C:\Users\97854\AppData\Roaming\Typora\typora-user-images\image-20230906163115279.png)

 可以写为$ L_{FL} = -(p_i^k)^γ* log(p_i^k)$

  注： inverse focal loss是与Focal loss反面出发

 焦点损失通过引入焦点因子来调整损失函数，以便更关注难以分类的样本，从而减轻了类别不平衡问题。焦点因子通常介于0和1之间，用于降低容易分类的样本的权重，同时增加难以分类的样本的权重。这使得模型更加关注那些容易混淆或分类错误的样本，从而提高了模型在少数类别上的性能。

 逆焦点损失是焦点损失的一种变种，其主要思想是反转焦点因子的作用。逆焦点损失通过将焦点因子的值设置为大于1的数来增加容易分类的样本的权重，同时将焦点因子的值设置为小于1的数来减少难以分类的样本的权重。这与标准的焦点损失相反，后者更加关注难以分类的样本。

 2. Class-balanced focal loss (CB)


 3. Distribution-balanced loss (DB)

 https://blog.csdn.net/weixin_42437114/article/details/127774342

  • 一点小思考

    1. 难样本问题

      难分类样本与易分类样本其实是一个动态概念，也就是说 $p_t$ 会随着训练过程而变化。原先易分类样本即$p_t$ 大的样本，可能随着训练过程变化为难训练样本即$p_t$ 小的样本。

    上面讲到，由于Loss梯度中，难训练样本起主导作用，即参数的变化主要是朝着优化难训练样本的方向改变。当参数变化后，可能会使原先易训练的样本$p_t$发生变化，即可能变为难训练样本。当这种情况发生时，可能会造成模型收敛速度慢，正如苏剑林在他的文章中提到的那样。

    为了防止难易样本的频繁变化，应当选取小的学习率。防止学习率过大，造成 $w$ 变化较大从而引起 $p_t$的巨大变化，造成难易样本的改变。

    1. 训练大模型时利用负样例和loss函数平滑的思想类似吗？

    2. 如何表示生成式大模型的置信度

      • 求和或平均：一种简单的方法是将所有token的logits相加或取平均。这可以给出一个粗略的整体置信度指标，但可能无法捕捉到序列中不同部分的重要性。

      • 加权平均：我们可以根据每个token的位置或其他因素给予不同的权重。例如，序列开始部分的token可能比后面的token更重要。

      • 序列模型：我们可以使用额外的序列模型（如RNN或Transformer）来处理整个logits序列，并输出一个整体置信度。

      • 注意力机制：我们可以使用注意力机制来确定模型应该关注序列中的哪些部分。这可以帮助模型更好地理解整个序列，并提高整体置信度的准确性。

      如何提高大模型的置信度

      如何让大模型认识到自己的知识边界